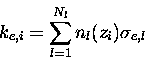 |
(7.32) |
Discretizing the spatial grid is accomplished by dividing the model atmosphere into Ni layers. This is done by specifying Ni+1 altitudes, not necessarily equally spaced, at which the solution will be determined. Each altitude level, or grid point, is assigned a value for all relevant quantities of the model atmosphere.
The extinction coefficient is calculated at each point on the
vertical grid using,
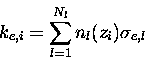 |
(7.32) |
![\begin{displaymath}\tau_i = \sum_{i'=i}^{N_i-1} \left[ \frac{ k_{e,i'} + k_{e,i'+1} }
{2} \right] (z_{i'+1} - z_{i'})
\end{displaymath}](img376.gif) |
(7.33) |
The source function is also taken as varying linearly through a layer,
i.e.
![]() .
Substituting this into
equations (4.26) and (4.27) gives an expression for the
Stokes vector coefficient
at i in terms of that at i+1 and a combination of the
source function coefficients at i and i+1 as follows,
.
Substituting this into
equations (4.26) and (4.27) gives an expression for the
Stokes vector coefficient
at i in terms of that at i+1 and a combination of the
source function coefficients at i and i+1 as follows,
| = | 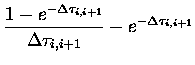 |
(7.36) | |
| = | 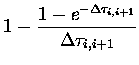 |
(7.37) |
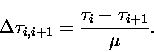 |
(7.38) |
The vertical resolution required is mainly a function of optical
depth and inhomogeneity of the atmosphere. Tests using different
vertical grids have revealed that a vertical spacing of 1 km is
more than adequate for most simulations.
Above the top of the ozone layer (![]() 45 km),
where the pressure is very small,
a larger grid spacing may be used as there is little scattering.
An exception to this includes modeling the limb. After corrections
for the sphericity of the Earth have been made (see Section 4.6),
where a spacing of 0.5 km may be necessary due to the longpath length
between layers. Another exception is when an optically thick aerosol
layer is present, such as tropospheric dust or marine aerosols in the
boundary layer.
45 km),
where the pressure is very small,
a larger grid spacing may be used as there is little scattering.
An exception to this includes modeling the limb. After corrections
for the sphericity of the Earth have been made (see Section 4.6),
where a spacing of 0.5 km may be necessary due to the longpath length
between layers. Another exception is when an optically thick aerosol
layer is present, such as tropospheric dust or marine aerosols in the
boundary layer.
To determine the validity of taking the source function as varying linearly
between levels, another method was tested.
The average source function of two adjacent levels was assumed to
be representative of the layer between them.
This simpler treatment gives the following constants,
| (7.39) |