Integration of all quantities over ![]() is also done numerically.
Gaussian-Quadrature is chosen as it has been proven to be superior
to other quadrature integration techniques (Liou, 1980).
In Gaussian-Quadrature, the discrete values of
is also done numerically.
Gaussian-Quadrature is chosen as it has been proven to be superior
to other quadrature integration techniques (Liou, 1980).
In Gaussian-Quadrature, the discrete values of ![]() are
determined by the roots of the Legendre polynomial of order 2Nj.
The weights, wj, have a more complicated origin but are
always normalized such that,
are
determined by the roots of the Legendre polynomial of order 2Nj.
The weights, wj, have a more complicated origin but are
always normalized such that,
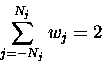 |
(7.40) |
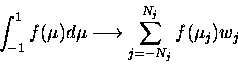 |
(7.41) |
For example, the source function of equation (4.28) becomes,
![\begin{displaymath}{\bf J}_{n+1}^{cm}(\tau_i;\mu_j) =
\frac{\tilde{\omega}(\tau_...
..._i;\mu_j;\mu_{j'}) {\bf I}_n^{sm}(\tau_i;\mu_{j'})] \, w_{j'}.
\end{displaymath}](img394.gif) |
(7.42) |
In the calculation of irradiance, the integration is only performed over one hemisphere. This presents no real problem as the summation can run from 1 to Nj. However, care must be taken to ensure that the sum of the weights is exactly unity. To ensure this in the code, a renormalization is performed.
One drawback of using Gaussian-Quadrature is that, as the pivots are prescribed, they rarely correspond to angles desired. One way around this is to add extra pivots at any desired angles. These will have a zero weighting associated with them as they should not influence the integration. One example of when this is useful is in the calculation of the Stokes vector near the limb.