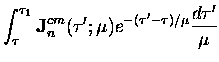Successive Orders of Scattering Solution
Technique

The method used to solve the radiative transfer equation, or the azimuthally independent version, is the successive orders of scattering technique. This is an iterative method in which the Stokes vector is calculated for photons scattered once, twice, three times, etc., with the total Stokes vector obtained as the sum over all orders (e.g.: Hansen and Travis, 1974). Based on physical arguments, this infinite series should converge. The upward and downward Stokes vector streams of scattering order n for even Fourier coefficient m are given by,

  

$${\b I}_n^{cm}(\tau;\mu) \int_{\tau}^{\tau_1} {\b J}_n^{cm}(\tau';\mu) e^{-(\tau'-\tau)/\mu} \frac{d\tau'}{\mu}$$ = (7.26)

$${\b I}_n^{cm}(\tau;-\mu) \int_0^{\tau} {\b J}^{cm}_n(\tau';-\mu) e^{-(\tau-\tau')/\mu} \frac{d\tau'}{\mu}$$ = (7.27)

where $n\geq1$, and the source function vector of order n+1 is given by,

$${\b J}_{n+1}^{cm}(\tau;\mu) = \frac{\tilde{\omega}}{2} \int_{... ...mu') - {\b Z}^{sm}(\mu;\mu') {\b I}_n^{sm}(\tau;\mu') ] d\mu'.$$ (7.28)

The zero-order Stokes vector is,

$${\b I}_0^{cm}(\tau;\mu) = \pi {\b F}_o e^{-\tau/\mu_o} \delta(\mu+\mu_o)$$ (7.29)

and so the first order source function vector is that for single scattering. The total Stokes vector is the sum over all orders,

$${\b I}^{cm}(\tau;\pm \mu) = \sum_{n=1}^{\infty} {\b I}_n^{cm}(\tau;\pm \mu).$$ (7.30)

There is an analogous set of equations for the odd expansion coefficients. In practice, the summation in Equation (4.30) is truncated once some convergence criterion is met. The condition implemented in the code is,

$$\left\vert \left\vert \frac{I_n^{cm}(\tau;\mu)}{\sum_{n'=1}^{n-1}I_{n'}^{cm}(\tau;\mu)} \right\vert \right\vert \leq 10^{-q}$$ (7.31)

where the $\Vert$ denotes largest over all $\tau$ and $\mu$ and the value of q is discussed below. The number of orders required to achieve this will be at least as large as the optical thickness for a near-conservative atmosphere. This method has the advantage of being conceptually simple as well as able to provide insight into the multiple scattering phenomena. In addition, it is applicable to inhomogeneous atmospheres and very amenable to spherical geometry corrections. Another advantage is that as the intensity has been expanded in a Fourier series, the high frequency terms arise from photons scattered a small number of times and so most Fourier terms can be accurately determined by computing only a few orders of scattering (Hansen and Travis, 1974). The main disadvantage of this method is that for optically thick, near-conservative atmospheres the number of orders required for convergence is prohibitive. Thus modeling of thick clouds, for example, is impractical. Although not used in this study, this restriction may be alleviated somewhat by implementing what is known as Lambda-iteration to speed up the orders of scattering convergence (Griffioen et al., 1994; Olson et al., 1986). Thus far, Lambda-iteration has only been applied to resonance line scattering as far as the author is aware.

The model has been run for homogeneous atmospheres consisting entirely of Rayleigh or Mie scattering. The Mie scatterers follow the standard-gamma size distribution with parameters $r_{\rm eff}=0.2~\mu$m and $v_{\rm eff}=0.07$. Each were run for atmospheres of optical depth 0.1, 1, and 10. In addition, the Rayleigh calculations were performed for single-scattering albedos of 1 and 0.8. The number of scattering orders required for convergence to q=2, 3, and 4, as per equation (4.31), are presented in Table 4.1. For thin atmospheres, the single scattering albedo did not effect the number of orders necessary for convergence. However, thick absorbing atmospheres required markedly fewer iterations, especially for the azimuthally independent coefficient.

 

Table 4.1: Number of scattering orders required for convergence for q=2,3,4 in homogeneous atmospheres as a function of expansion coefficient and vertical optical depth.

 

Expansion
Coefficient	$\tau_1=0.1$	$\tau_1=1$	$\tau_1=10$
	Rayleigh, $\tilde{\omega}=1$
m=0	4,5,7	10,15,21	68,137,213
m=1	3,4,6	7,10,13	20,28,34
m=2	3,4,5	6,8,11	19,25,31
	Rayleigh, $\tilde{\omega}=0.8$
m=0	4,5,6	8,11,15	25,36,45
m=1	2,4,5	6,8,10	15,20,24
m=2	3,4,5	5,7,9	14,18,23
	Mie, $\tilde{\omega}=1$
m=0	5,6,7	11,16,21	45,83,128
m=1	8,10,11	10,14,17	24,31,38
m=2	5,6,7	9,11,14	17,22,27
m=3	5,6,6	9,11,13	18,20,23
m=4	4,5,6	5,7,8	8,10,12

Examining results from the conservative Rayleigh atmosphere, the accuracy of the q=2 and q=3 conditions were assessed by comparing the reflected intensities and linear polarizations with that using the q=4 condition. The maximum percent differences are given in Table 4.2. Differences in intensity were observed to roughly increase linearly with optical depth, with the q=3 condition an order of magnitude better than q=2. Differences in polarization were found to be smaller overall and they increased with optical depth at a slower rate. This is probably due to the fact that the polarization is a ratio of intensities and there should be some offsetting of errors in the numerator and denominator. Values of polarization less than 0.001 were excluded from the comparison as small absolute differences will lead to large relative differences. The maximum differences were observed to be smaller for non-conservative atmospheres as fewer orders of scattering are necessary.

As a result, the following conditions have been implemented in the model. For $\tau_1 \leq 1$, q=2 is used and for $\tau_1>1$, q=2.5 is used. In the wavelength range relevant to this study, namely 300-800 nm, optical depths larger than unity will normally be encountered at wavelengths shortward of 320 nm. In this region ozone absorbs strongly so the single scattering albedo will be substantially less than unity.

 

Table 4.2: Maximum difference in q=2 and q=3 reflected intensities and linear polarizations as compared to to q=4.

 

Optical	Convergence	Percent Difference in:
Depth	Criterion	Intensity	Linear Polarization
$\tau_1=0.1$	q=2	0.092	0.010
	q=3	0.014	0.002
$\tau_1=1$	q=2	1.882	0.082
	q=3	0.185	0.044
$\tau_1=10$	q=2	8.558	0.321
	q=3	0.884	0.190

Once the convergence criterion has been reached and all expansion coefficients have been computed, the total Stokes vector can be determined using equation (4.13) for the desired viewing geometry. Note that as the solution method is an iterative one, the coupling of the even and odd source terms for a given harmonic, as mentioned above, does not impose any practical difficulties as each is only a function of the (calculated) previous order of the Stokes vector.