


Next: Successive Orders of Scattering
Up: Model Description
Previous: Combined Rayleigh and Mie
It will prove useful to expand the azimuthal dependence of the
Stokes vector and phase matrix in a Fourier cosine and sine series in
order to reduce the number of variables treated at any one time. Thus,
where m is the harmonic index and M is the highest harmonic
used in the expansion.
In general an infinite number of terms is required to exactly
represent the the phase matrix. In practice, however, the summation
is truncated at M and its value is dependent upon the nature
of the scatterers. For isotropic scatterers, which have azimuthally
independent phase matrix elements, only the m=0 term is required for an exact
series representation. Rayleigh scatterers require terms up to m=2.
The number required for Mie scattering will be highly dependent upon
the size to wavelength ratio. For example,
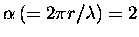 (where
(where 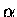 is the size parameter as defined in Section 2.4.1),
terms up to m=8 will suffice while for
is the size parameter as defined in Section 2.4.1),
terms up to m=8 will suffice while for 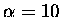 terms up to
m=16 are required. In addition, if only the irradiance or mean radiance
are desired, then only the m=0 term need be computed as these are
azimuthally independent quantities.
terms up to
m=16 are required. In addition, if only the irradiance or mean radiance
are desired, then only the m=0 term need be computed as these are
azimuthally independent quantities.
The azimuthally independent phase matrix coefficients must be
calculated. This is done by making use of the orthogonality
of sines and cosines. For example,
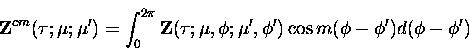 |
(7.14) |
with an analogous expression for odd coefficients.
Many Fourier coefficients of the various phase matrix elements will end
up being zero as all elements are either even or odd functions of
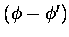 .
The elements of
.
The elements of 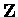 are even or odd according to,
are even or odd according to,
![\begin{displaymath}\left[ \begin{array}{cccc}
e & e & o & - \\
e & e & o & o \\
o & o & e & e \\
- & o & e & e \\
\end{array} \right]
\end{displaymath}](img329.gif) |
(7.15) |
where e denotes an even function and o an odd function.
Upon substituting these expansions into the plane-parallel
radiative transfer equation, rewritten with the source term shown
explicitly,
 |
(7.16) |
the following set
of differential equations relating the expansion coefficients for a
given harmonic are obtained,
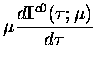 |
= |
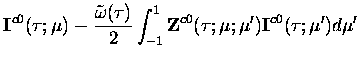 |
(7.17) |
 |
= |
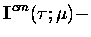 |
(7.18) |
| |
|
![$\displaystyle \frac{\tilde{\omega}(\tau)}{2} \int_{-1}^1
[{\bf Z}^{cm}(\tau;\mu...
...I}^{cm}(\tau;\mu') -
{\bf Z}^{sm}(\tau;\mu;\mu') {\bf I}^{sm}(\tau;\mu')] d\mu'$](img335.gif) |
|
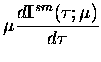 |
= |
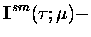 |
(7.19) |
| |
|
![$\displaystyle \frac{\tilde{\omega}(\tau)}{2} \int_{-1}^1
[{\bf Z}^{sm}(\tau;\mu...
...I}^{cm}(\tau;\mu') +
{\bf Z}^{cm}(\tau;\mu;\mu') {\bf I}^{sm}(\tau;\mu')] d\mu'$](img338.gif) |
|
where
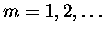 The single radiative transfer equation has been
decomposed into 2M+1 azimuthally independent equations.
Also, Equations (4.18) and (4.19) are coupled in
The single radiative transfer equation has been
decomposed into 2M+1 azimuthally independent equations.
Also, Equations (4.18) and (4.19) are coupled in
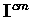 and
and
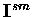 .
.
Equations (4.17)-(4.19) have been recast in
integral form below through the use of the integrating factor
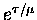 .
Only the downward streams are given,
.
Only the downward streams are given,
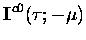 |
= |
 |
(7.20) |
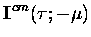 |
= |
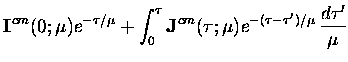 |
(7.21) |
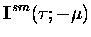 |
= |
 |
(7.22) |
and the upward streams may be likewise determined from
equations (4.17)-(4.19) using the
integrating factor
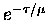 .
Also, the following definitions have been used,
.
Also, the following definitions have been used,
in order to simplify these and future equations.



Next: Successive Orders of Scattering
Up: Model Description
Previous: Combined Rayleigh and Mie
Chris McLinden
1999-07-22
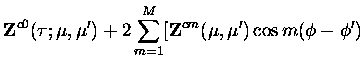

![\begin{displaymath}\left[ \begin{array}{cccc}
e & e & o & - \\
e & e & o & o \\
o & o & e & e \\
- & o & e & e \\
\end{array} \right]
\end{displaymath}](img329.gif)

![]() .
Only the downward streams are given,
.
Only the downward streams are given,

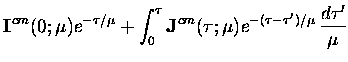

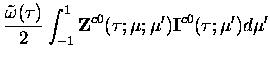
![$\displaystyle \frac{\tilde{\omega}(\tau)}{2} \int_{-1}^1
[{\bf Z}^{cm}(\tau;\mu...
...u') -
{\bf Z}^{sm}(\tau;\mu;\mu') {\bf I}^{sm}(\tau;\mu')] d\mu' \,\,\,\,\,\,\,$](img352.gif)
![$\displaystyle \frac{\tilde{\omega}(\tau)}{2} \int_{-1}^1
[{\bf Z}^{sm}(\tau;\mu...
...u') +
{\bf Z}^{cm}(\tau;\mu;\mu') {\bf I}^{sm}(\tau;\mu')] d\mu' \,\,\,\,\,\,\,$](img354.gif)