


Next: Rayleigh Scattering
Up: Types of Scattering
Previous: Types of Scattering
Mie Scattering
Mie scattering is the straightforward (if somewhat painful) application
of Maxwell's equations to an isotropic, homogeneous, dielectric sphere.
It will be the first type of scattering examined as it is
equally applicable to spheres of all sizes, refractive indices and for
radiation at all wavelengths.
Briefly, Maxwell's equations are solved in spherical co-ordinates through
separation of variables. The incident plane wave is expanded in
Legendre polynomials so the solutions inside and outside the sphere can
be matched at the boundary. The solution sought is at a distance
much larger than the wavelength,
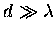 ,
in the so-called
far-field zone.
The far-field solution is expressed in terms
of two scattering functions,
,
in the so-called
far-field zone.
The far-field solution is expressed in terms
of two scattering functions,
and where 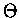 is the scattering angle.
These infinite series can be physically interpreted as a multiple expansion
of scattered light (Hansen and Travis, 1974).
Thus, the a1 coefficient specifies
the amount of electric dipole radiation.
The functions
is the scattering angle.
These infinite series can be physically interpreted as a multiple expansion
of scattered light (Hansen and Travis, 1974).
Thus, the a1 coefficient specifies
the amount of electric dipole radiation.
The functions  and
and 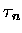 are given by,
are given by,
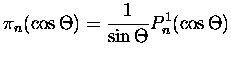 |
|
|
(3.27) |
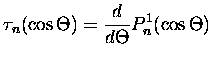 |
|
|
(3.28) |
where Pn1 are associated Legendre polynomials of the first kind.
Also,
| an |
= |
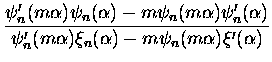 |
(3.29) |
| bn |
= |
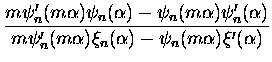 |
(3.30) |
where
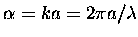 is called the size parameter,
m is the index of refraction, a is the particle radii,
and
is called the size parameter,
m is the index of refraction, a is the particle radii,
and 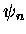 and
and 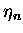 are related to spherical Bessel
functions. They are characteristic of spherical geometry and arise
when solving the wave equation. The prime indicates the first derivative
with respect to r.
The majority of the effort in carrying out Mie calculations is in determining
the coefficients an and bn.
are related to spherical Bessel
functions. They are characteristic of spherical geometry and arise
when solving the wave equation. The prime indicates the first derivative
with respect to r.
The majority of the effort in carrying out Mie calculations is in determining
the coefficients an and bn.
Using these scattering functions, the scattered components of the
electric field can be expressed in terms of the incident components,
![\begin{displaymath}\left[
\begin{array}{c}
E_l^s \\
E_r^s \\
\end{array}\right...
...left[
\begin{array}{c}
E_l^i \\
E_r^i \\
\end{array}\right].
\end{displaymath}](img146.gif) |
(3.31) |
Using equation (2.2), equation (2.31) can
expressed in terms of an incident and scattered Stokes vector.
They are related by the Mie scattering matrix,
![\begin{displaymath}{\b P}(\Theta) =
\left[
\begin{array}{c c c c}
P_{11}(\Theta...
...0 & 0 & -P_{34}(\Theta)& P_{33}(\Theta) \\
\end{array}\right]
\end{displaymath}](img147.gif) |
(3.32) |
where the four independent Mie scattering matrix elements are,
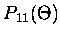 |
= |
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [\vert S_1(\Theta)\vert^2 +
\vert S_2(\Theta)\vert^2]$](img149.gif) |
(3.33) |
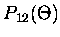 |
= |
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [\vert S_2(\Theta)\vert^2 -
\vert S_1(\Theta)\vert^2]$](img151.gif) |
(3.34) |
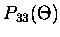 |
= |
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [S_2(\Theta)S_1^*(\Theta) +
S_1(\Theta)S_2^*(\Theta)]$](img153.gif) |
(3.35) |
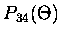 |
= |
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [S_2(\Theta)S_1^*(\Theta) -
S_1(\Theta)S_2^*(\Theta)]$](img155.gif) |
(3.36) |
The Mie scattering, absorption, and extinction cross-sections can all
be expressed in terms of the an and bn coefficients,
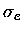 |
= |
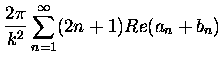 |
(3.37) |
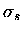 |
= |
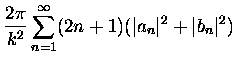 |
(3.38) |
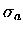 |
= |
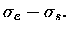 |
(3.39) |
Another useful quantity is the asymmetry factor, g, which is also the
first moment of the phase function,
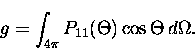 |
(3.40) |
The asymmetry factor describes the shape of the phase function;
g>1 indicates forward scattering is favoured while g<1 indicates
backscattering is favoured. It is a useful parameter for characterizing
the phase function independent of scattering angle.
The Mie asymmetry factor can be expressed as,
![\begin{displaymath}g = 2 \sum_{n=1}^{\infty} \left[ \frac{n(n+2)}{n+1} Re(a_n a_...
... +
b_n b_{n+1}^*) + \frac{2n+1}{n(n+1)} Re(a_n+b_n^*) \right].
\end{displaymath}](img163.gif) |
(3.41) |
The number of terms required in these summations is slightly
larger than the size parameter, 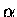 (Hansen and Travis, 1974).
For example, for a particle of radius 1
(Hansen and Travis, 1974).
For example, for a particle of radius 1 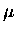 m at 500 nm,
approximately 13 terms are necessary.
m at 500 nm,
approximately 13 terms are necessary.
Assuming initially unpolarized light,
![${\b I_o}=[I_o,0,0,0]^{T}$](img165.gif) ,
after a scattered event the Stokes vector will have the form
,
after a scattered event the Stokes vector will have the form
![${\b I}=[P_{11}I_o,P_{12}I_o,0,0]^{T}$](img166.gif) .
Hence, the degree of linear polarization as a function of scattering
angle is,
.
Hence, the degree of linear polarization as a function of scattering
angle is,
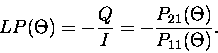 |
(3.42) |
All the Mie quantities discussed thus far have been for a single size
parameter, and hence a particular radius. As will be discussed in section
2.5,
a typical aerosol mass will contain a wide range of sizes. Hence,
Mie cross-sections and scattering matrix elements must be
averaged over a particle size distribution, n(r).
The scattering matrix elements transform as,
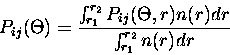 |
(3.43) |
where n(r) is the particle size distribution of equation (2.60) or
(2.61) and
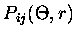 is the ij element of the
scattering matrix, explicitly showing the particle radius dependence.
It is characterized by peaks
in the forward scattering and, to a lesser extent, backward scattering
directions. In addition, there is fine structure throughout, indicative
of constructive and destructive interference effects (although when
averaged over a wide size distribution much of this detailed structure
is lost).
The large forward scattering peak can be understood qualitatively
as follows. If the smallest of scatterers can be represented by a
single dipole, then larger scatterers can be represented by a collection
of dipoles, with the required number increasing with larger particles size.
It is a well known result that for more than one dipole, randomly distributed,
the only direction in which the interference is totally constructive is the
forward direction (Jackson, 1962).
is the ij element of the
scattering matrix, explicitly showing the particle radius dependence.
It is characterized by peaks
in the forward scattering and, to a lesser extent, backward scattering
directions. In addition, there is fine structure throughout, indicative
of constructive and destructive interference effects (although when
averaged over a wide size distribution much of this detailed structure
is lost).
The large forward scattering peak can be understood qualitatively
as follows. If the smallest of scatterers can be represented by a
single dipole, then larger scatterers can be represented by a collection
of dipoles, with the required number increasing with larger particles size.
It is a well known result that for more than one dipole, randomly distributed,
the only direction in which the interference is totally constructive is the
forward direction (Jackson, 1962).
Similarly, the cross-sections and asymmetry factor transform as,
Usually, the size distribution is normalized such that the denominator
in equations (2.43)-(2.45) are unity.



Next: Rayleigh Scattering
Up: Types of Scattering
Previous: Types of Scattering
Chris McLinden
1999-07-22
![]() ,
in the so-called
far-field zone.
The far-field solution is expressed in terms
of two scattering functions,
,
in the so-called
far-field zone.
The far-field solution is expressed in terms
of two scattering functions,
![$\displaystyle \sum_{n=1}^{\infty}\frac{2n+1}{n(n+1)}
[a_n \pi_n(\cos\Theta) + b_n \tau_n(\cos\Theta)]$](img133.gif)
![$\displaystyle \sum_{n=1}^{\infty}\frac{2n+1}{n(n+1)}
[b_n \pi_n(\cos\Theta) + a_n \tau_n(\cos\Theta)]$](img135.gif)
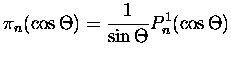
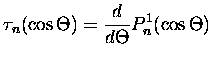
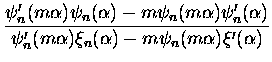
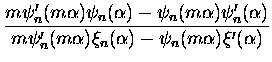
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [\vert S_1(\Theta)\vert^2 +
\vert S_2(\Theta)\vert^2]$](img149.gif)
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [\vert S_2(\Theta)\vert^2 -
\vert S_1(\Theta)\vert^2]$](img151.gif)
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [S_2(\Theta)S_1^*(\Theta) +
S_1(\Theta)S_2^*(\Theta)]$](img153.gif)
![$\displaystyle \frac{2\pi}{k^2\sigma_s} [S_2(\Theta)S_1^*(\Theta) -
S_1(\Theta)S_2^*(\Theta)]$](img155.gif)
![\begin{displaymath}g = 2 \sum_{n=1}^{\infty} \left[ \frac{n(n+2)}{n+1} Re(a_n a_...
... +
b_n b_{n+1}^*) + \frac{2n+1}{n(n+1)} Re(a_n+b_n^*) \right].
\end{displaymath}](img163.gif)
![]() (Hansen and Travis, 1974).
For example, for a particle of radius 1
(Hansen and Travis, 1974).
For example, for a particle of radius 1 ![]() m at 500 nm,
approximately 13 terms are necessary.
m at 500 nm,
approximately 13 terms are necessary.
![]() ,
after a scattered event the Stokes vector will have the form
,
after a scattered event the Stokes vector will have the form
![]() .
Hence, the degree of linear polarization as a function of scattering
angle is,
.
Hence, the degree of linear polarization as a function of scattering
angle is,