For many applications, calculations using plane-parallel geometry is adequate.
However, for solar zenith angles larger than 75![]() the attenuation
of the direct solar beam is overestimated in a plane-parallel atmosphere.
This is because as
the attenuation
of the direct solar beam is overestimated in a plane-parallel atmosphere.
This is because as ![]() tends towards zero, the plane parallel
pathlength enhancement,
tends towards zero, the plane parallel
pathlength enhancement, ![]() ,
becomes infinite.
Also, for solar zenith angles larger than 90
,
becomes infinite.
Also, for solar zenith angles larger than 90![]() ,
some parts of the
atmosphere will still be directly illuminated which is not possible
using plane parallel geometry.
Similar problems arise in the calculation of scattered light
near the limb, or horizon. Pathlengths can be both overestimated or
underestimated, depending on whether the streams are upward or downward.
In a plane-parallel atmosphere, any viewing direction below the
horizon will have a direct surface component.
In a spherical atmosphere, for an observation made at 20 km,
there is no direct surface component until 4.5
,
some parts of the
atmosphere will still be directly illuminated which is not possible
using plane parallel geometry.
Similar problems arise in the calculation of scattered light
near the limb, or horizon. Pathlengths can be both overestimated or
underestimated, depending on whether the streams are upward or downward.
In a plane-parallel atmosphere, any viewing direction below the
horizon will have a direct surface component.
In a spherical atmosphere, for an observation made at 20 km,
there is no direct surface component until 4.5![]() below the local horizon.
below the local horizon.
These deficiencies are illustrated in Figure 4.2. The dashed lines represent a plane-parallel atmosphere superimposed on the spherical one (solid lines). Light scattered downward is over-attenuated in a plane-parallel atmosphere while light scattered upward is both under-attenuated and possesses a direct surface component.
To remedy these inadequacies a number of options are available.
One possibility is to solve the radiative transfer equation in
three-dimensional spherical coordinates. The drawback of
this is the huge increase in both complexity of the solution and
computation time required.
The alternative adopted herein is to integrate the source function
through a series of spherical shells similar to that depicted in Figure 4.2.
In this formulation, the
physical distance between layers is no longer simply
![]() ,
but a more complicated function of
,
but a more complicated function of ![]() and altitude.
and altitude.
In practice, equations (4.34) and (4.35) are still used.
However, the definition
of
![]() is modified to,
is modified to,
| (7.43) |
| (7.44) |
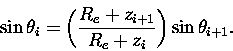 |
(7.46) |
In addition, a distinction must be made between upward radiance streams which
originate at the surface and upward radiance streams which
originate at the top of the atmosphere (originally as downward streams).
Radiance streams will originate from the surface
as long as
![]() and streams will originate from the
top of the atmosphere if
zt,i > 0. If the latter case is true then
at some point in the integration along the path, the tangent height will be
reached. If it does not correspond exactly to a vertical grid point then
a dummy grid point is created between levels.
Source function and extinction values are linearly interpolated onto it.
Similarly, the solar zenith angle will vary along the line-of-sight.
This correction has not been performed but it should not matter as long
as the sun is fairly high in the sky. Only if the line-of-sight passes
through the terminator is this correction important.
and streams will originate from the
top of the atmosphere if
zt,i > 0. If the latter case is true then
at some point in the integration along the path, the tangent height will be
reached. If it does not correspond exactly to a vertical grid point then
a dummy grid point is created between levels.
Source function and extinction values are linearly interpolated onto it.
Similarly, the solar zenith angle will vary along the line-of-sight.
This correction has not been performed but it should not matter as long
as the sun is fairly high in the sky. Only if the line-of-sight passes
through the terminator is this correction important.
Two checks are available to ensure the spherical and plane-parallel
versions are consistent: for high sun and viewing away from the limb,
the two should yield the same solution; and for
![]() ,
the two must also yield the same solution. These tests have been
performed and both plane-parallel and spherical versions give
nearly identical radiances.
,
the two must also yield the same solution. These tests have been
performed and both plane-parallel and spherical versions give
nearly identical radiances.