As mentioned in Section 2.2.1, the Stokes vector,
![]() ,
is always defined
with respect to a reference plane which is given by the
vertical direction and the direction of propagation,
the meridian plane.
However, the scattering matrix, as discussed in Section 2.3.4, was
referenced
to the plane of scattering. That is, the plane containing both the incident
and scattered directions. Thus, in order to compute the amount of light
incident in direction
,
is always defined
with respect to a reference plane which is given by the
vertical direction and the direction of propagation,
the meridian plane.
However, the scattering matrix, as discussed in Section 2.3.4, was
referenced
to the plane of scattering. That is, the plane containing both the incident
and scattered directions. Thus, in order to compute the amount of light
incident in direction
![]() and scattered into direction
and scattered into direction
![]() ,
,
![]() must first be transformed from the incident
meridian plane to the plane of scattering so that the scattering calculations
can be carried out and then from the plane of scattering to the scattered
meridian plane.
must first be transformed from the incident
meridian plane to the plane of scattering so that the scattering calculations
can be carried out and then from the plane of scattering to the scattered
meridian plane.
The Stokes vector can be rotated through an angle ![]() in
the anti-clockwise direction, when looking into the direction of propagation,
by the rotation matrix (e.g.: Liou, 1980),
in
the anti-clockwise direction, when looking into the direction of propagation,
by the rotation matrix (e.g.: Liou, 1980),
![\begin{displaymath}{\b L}(i) = \left[ \begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & ...
...sin 2i & \cos 2i & 0 \\
0 & 0 & 0 & 1 \\
\end{array} \right]
\end{displaymath}](img299.gif) |
(7.1) |
Applying both required rotations and grouping the scattering and
rotation matrices together, the phase matrix is arrived at,
| (7.2) |
![$\displaystyle \left[
\begin{array}{c c c c}
\pa & \pb c_1 & \pb s_1 & 0 \\
\pb...
..._1 + c_2 \pc c_1 & -\pd c_2 \\
0 & -\pd s_1 & \pd c_1 & \pc
\end{array}\right]$](img304.gif) |
|||
| c1 | = | (7.4) | |
| c2 | = | (7.5) | |
| s1 | = | (7.6) | |
| s2 | = | (7.7) |
The angles i1 and i2 can be related to the incident and scattered
directions,
![]() and
and
![]() ,
respectively, using spherical
trigonometry, as illustrated in Figure 4.1,
,
respectively, using spherical
trigonometry, as illustrated in Figure 4.1,
| = | 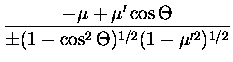 |
(7.8) | |
| = | 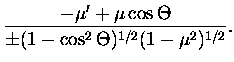 |
(7.9) |
| (7.10) |