


Next: Related Quantities
Up: Representation of Polarized Radiation
Previous: Representation of Polarized Radiation
Stokes Parameters
The representation of polarized radiation described above can be
cumbersome.
At this point the concept of independent scattering is
introduced. Independent scattering requires that interference of light
scattered by different particles be undetectable (Hansen and Travis, 1974).
The necessary condition for this to hold is that the scatterers must be
separated by a few times their radius.
To examine this, consider air at surface pressure,
which has a number density, N, of about
 molecules
molecules cm-3.
The mean intermolecular distance is
cm-3.
The mean intermolecular distance is
 (Mihalas, 1978) or 4.5 nm which is a factor of 60
larger than the `radius' of a nitrogen molecule.
(Mihalas, 1978) or 4.5 nm which is a factor of 60
larger than the `radius' of a nitrogen molecule.
A consequence of independent scattering is that light may be
described in the intensity domain and it will
prove useful to adopt an alternate representation, known
as Stokes parameters. The Stokes parameters are contained in a
4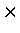 1 column matrix, called the Stokes vector,
1 column matrix, called the Stokes vector,
![\begin{displaymath}{\b I} = \left[ \begin{array}{c}
I \\
Q \\
U \\
V \\
\en...
...ft[ \begin{array}{cccc}
I & Q & U & V
\end{array} \right]^{T}
\end{displaymath}](img73.gif) |
(3.3) |
where
![$[\hspace{1em}]^{T}$](img74.gif) denotes transpose. The Stokes vector will often
be denoted as the transpose of a 1
denotes transpose. The Stokes vector will often
be denoted as the transpose of a 1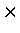 4 row matrix for the
sake of brevity.
Each element of the Stokes matrix can be written in terms of the
time averages of the parallel and perpendicular components of the
electric field,
4 row matrix for the
sake of brevity.
Each element of the Stokes matrix can be written in terms of the
time averages of the parallel and perpendicular components of the
electric field,
| I |
= |
 |
(3.4) |
| Q |
= |
 |
(3.5) |
| U |
= |
 |
(3.6) |
| V |
= |
 |
(3.7) |
where the asterisk represents the complex conjugate and <>
identifies a time average.
Each component has units of radiant intensity, or radiance
(i.e. 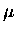 W
W cm
cm
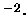 nm
nm
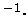 sr-1).
Radiance describes the amount of radiant energy passing normally
through a
differential area element in a direction confined to a differential solid
angle element per unit time per unit wavelength interval.
The Stokes representation is advantageous as all elements possess the same
units and are real and measurable quantities. The Stokes elements
for a single simple wave are related by
I2 = Q2 + U2 + V2.
After taking time averages, this identity becomes,
sr-1).
Radiance describes the amount of radiant energy passing normally
through a
differential area element in a direction confined to a differential solid
angle element per unit time per unit wavelength interval.
The Stokes representation is advantageous as all elements possess the same
units and are real and measurable quantities. The Stokes elements
for a single simple wave are related by
I2 = Q2 + U2 + V2.
After taking time averages, this identity becomes,
 .
The physical interpretation of each element is given below.
The first, I, describes the total (polarized and unpolarized)
radiance. If polarization is neglected, the Stokes vector reduces
to the single element, I.
The second, Q, is the radiance linearly polarized in the
direction parallel or perpendicular to the reference plane.
The third, U, is the radiance linearly polarized in the directions
45
.
The physical interpretation of each element is given below.
The first, I, describes the total (polarized and unpolarized)
radiance. If polarization is neglected, the Stokes vector reduces
to the single element, I.
The second, Q, is the radiance linearly polarized in the
direction parallel or perpendicular to the reference plane.
The third, U, is the radiance linearly polarized in the directions
45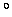 to the reference plane, and the fourth, V, is the radiance
circularly polarized.
to the reference plane, and the fourth, V, is the radiance
circularly polarized.
Natural sunlight is an example of completely unpolarized light and
so it could be represented by
![${\b I}=[I,0,0,0]^T$](img82.gif) .
In general, however,
light
is partially polarized and so it consists of polarized and unpolarized
components,
I=Ipol + Iunpol. The degree of
polarization, or fraction polarized, is defined as Ipol/I.
.
In general, however,
light
is partially polarized and so it consists of polarized and unpolarized
components,
I=Ipol + Iunpol. The degree of
polarization, or fraction polarized, is defined as Ipol/I.
In terms of the Stokes components, the degree of polarization, P,
is given by,
 |
(3.8) |
and the degree, of linear polarization, LP, is
 |
(3.9) |
If U is much smaller than Q, an alternative definition is employed,
LP=-Q/I, which preserves the sign of Q.
Similarly, the degree of circular polarization, CP, is
 |
(3.10) |
and the direction of polarization is given by the angle  ,
,
 |
(3.11) |
The radiance components parallel and perpendicular to the plane of
reference can also be expressed in terms of the Stokes parameters,



Next: Related Quantities
Up: Representation of Polarized Radiation
Previous: Representation of Polarized Radiation
Chris McLinden
1999-07-22
![]() molecules
molecules![]() cm-3.
The mean intermolecular distance is
cm-3.
The mean intermolecular distance is
![]() (Mihalas, 1978) or 4.5 nm which is a factor of 60
larger than the `radius' of a nitrogen molecule.
(Mihalas, 1978) or 4.5 nm which is a factor of 60
larger than the `radius' of a nitrogen molecule.
![]() 1 column matrix, called the Stokes vector,
1 column matrix, called the Stokes vector,
![\begin{displaymath}{\b I} = \left[ \begin{array}{c}
I \\
Q \\
U \\
V \\
\en...
...ft[ \begin{array}{cccc}
I & Q & U & V
\end{array} \right]^{T}
\end{displaymath}](img73.gif)
![]() .
In general, however,
light
is partially polarized and so it consists of polarized and unpolarized
components,
I=Ipol + Iunpol. The degree of
polarization, or fraction polarized, is defined as Ipol/I.
.
In general, however,
light
is partially polarized and so it consists of polarized and unpolarized
components,
I=Ipol + Iunpol. The degree of
polarization, or fraction polarized, is defined as Ipol/I.


