


Next: Depolarization by Air
Up: Types of Scattering
Previous: Mie Scattering
The scattering of light by gases was first treated quantitatively by
Lord Rayleigh in 1871 in an effort to explain the blue colour of the sky
and the red colour of the sunset.
There are numerous ways of arriving at the equation which governs
Rayleigh scattering.
Classical EM theory can be employed using the far-field solution while
retaining only the dipole term (e.g.: Jackson, 1962).
Quantum mechanical perturbation theory
for two-photon elastic processes provides both a powerful and elegant
means (e.g.: Craig and Thirunamachandran, 1984).
In order for Rayleigh scattering to be valid, the size of the
particle must be much smaller than the wavelength of the incident
radiation, both inside and outside of the particle. These conditions
can be expressed as,
where m is the refractive index.
Rayleigh scattering theory is applicable to scattering of UV and visible
radiation by air molecules, infra-red radiation by small aerosols,
and microwave radiation by cloud and rain drops. Practical
applications of Rayleigh scattering include lidar, weather radar, and
remote sounding of cloud water.
The route adopted herein is to consider the limiting case of Mie
scattering.
When equation (2.46) is valid, only the n=1 term in the
Mie scattering functions need be retained so that,
![$\displaystyle S_1(\Theta) \simeq \frac{3}{2} [a_1 \pi_1(\Theta) + b_1 \tau_1(\Theta)]$](img178.gif) |
|
|
(3.48) |
![$\displaystyle S_2(\Theta) \simeq \frac{3}{2} [b_1 \pi_1(\Theta) + a_1 \tau_1(\Theta)]$](img179.gif) |
|
|
(3.49) |
where
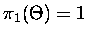 ,
,
 and
and
 .
Furthermore,
if equation (2.47) is valid, then
.
Furthermore,
if equation (2.47) is valid, then
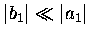 and hence,
and hence,
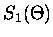 |
= |
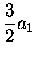 |
(3.50) |
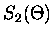 |
= |
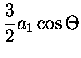 |
(3.51) |
| a1 |
= |
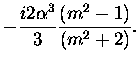 |
(3.52) |
Using equation (2.32), the Rayleigh scattering matrix has the
form
![\begin{displaymath}{\b P}(\Theta) = \frac{3}{2}
\left[
\begin{array}{c c c c}
\f...
...os\Theta & 0 \\
0 & 0 & 0 & \cos\Theta \\
\end{array}\right]
\end{displaymath}](img187.gif) |
(3.53) |
and from equation (2.39), the Rayleigh scattering cross-section
is,
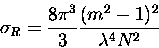 |
(3.54) |
where the approximation has been made,
 ,
and N is the
number of molecules per unit volume at standard temperature and
pressure.
The
,
and N is the
number of molecules per unit volume at standard temperature and
pressure.
The
 dependence
is a very important property of molecular scattering and is the
reason why optical depth varies by a factor of 10 throughout the
visible spectral region.
The Rayleigh asymmetry factor is zero as forward and backward
scattering are equally probable. Note that if the index of
refraction has an imaginary component, then the Rayleigh absorption
cross-section will be non-zero and can be determined in a similar
manner using equation (2.39). While air consists of many
species which absorb in the visible and near-UV,
it is convenient to treat this separately and so the refractive index
of air is taken to be real.
dependence
is a very important property of molecular scattering and is the
reason why optical depth varies by a factor of 10 throughout the
visible spectral region.
The Rayleigh asymmetry factor is zero as forward and backward
scattering are equally probable. Note that if the index of
refraction has an imaginary component, then the Rayleigh absorption
cross-section will be non-zero and can be determined in a similar
manner using equation (2.39). While air consists of many
species which absorb in the visible and near-UV,
it is convenient to treat this separately and so the refractive index
of air is taken to be real.



Next: Depolarization by Air
Up: Types of Scattering
Previous: Mie Scattering
Chris McLinden
1999-07-22
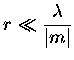
![$\displaystyle S_1(\Theta) \simeq \frac{3}{2} [a_1 \pi_1(\Theta) + b_1 \tau_1(\Theta)]$](img178.gif)
![$\displaystyle S_2(\Theta) \simeq \frac{3}{2} [b_1 \pi_1(\Theta) + a_1 \tau_1(\Theta)]$](img179.gif)