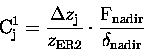Next: Simulations Using Synthetic Spectra
Up: Trace-Gas Retrievals
Previous: Calculation of Air Mass
Retrieval Algorithm
This section outlines the method used to retrieve
vertical profiles of O3, NO2, and BrO from measured
ACDs. A more compact notation is now adopted: let 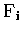 represent the measured ACD at elevation angle i
and
represent the measured ACD at elevation angle i
and
 represent the ACD in the reference, initially
an unknown.
Hence the total ACD at elevation angle i is
represent the ACD in the reference, initially
an unknown.
Hence the total ACD at elevation angle i is
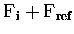 .
This is related to the vertical column amounts through,
.
This is related to the vertical column amounts through,
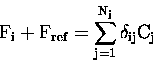 |
(11.17) |
where
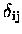 is the air mass factor weighting matrix
(also known as the kernel) at elevation angle i
for an absorber in layer j,
is the air mass factor weighting matrix
(also known as the kernel) at elevation angle i
for an absorber in layer j, 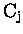 is the vertical column density
in layer j, and the sum is over
is the vertical column density
in layer j, and the sum is over 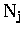 vertical layers.
Hence each ACD is the weighted sum of contributions from all
layers. Before being able to solve for
vertical layers.
Hence each ACD is the weighted sum of contributions from all
layers. Before being able to solve for 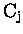 ,
the column abundance in the reference must be determined. As the
majority of the ER-2 flights occurred when the sun was fairly high
in the sky (
,
the column abundance in the reference must be determined. As the
majority of the ER-2 flights occurred when the sun was fairly high
in the sky (
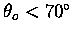 )
and the reference is composed
almost entirely of direct sunlight, the slant path enhancement
for the reference through all layers above the aircraft is well approximated
as
)
and the reference is composed
almost entirely of direct sunlight, the slant path enhancement
for the reference through all layers above the aircraft is well approximated
as
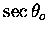 .
As such,
.
As such,
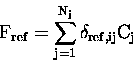 |
(11.18) |
where
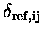 is the reference air mass factor matrix which
has the simple form,
is the reference air mass factor matrix which
has the simple form,
![\begin{displaymath}{\rm\delta_{ref,ij}} =
\left[
\begin{array}{c\vert ccccccc} ...
...\sec{\theta_o} & \cdots &\sec{\theta_o} \\
\end{array}\right]
\end{displaymath}](img623.gif) |
(11.19) |
and 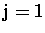 to
to
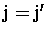 are the layers below the aircraft and
are the layers below the aircraft and
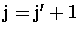 to
to
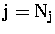 are the layers above the aircraft.
The column abundance in the reference has simply been expressed as the
sum of the vertical column in the layers above the aircraft multiplied by the
are the layers above the aircraft.
The column abundance in the reference has simply been expressed as the
sum of the vertical column in the layers above the aircraft multiplied by the
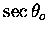 pathlength enhancement factor. Thus, equation (6.17)
can be expressed as,
pathlength enhancement factor. Thus, equation (6.17)
can be expressed as,
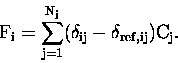 |
(11.20) |
The main advantage of this formulation is that the column density
in the reference need not be solved for prior to the inversion.
The use of the horizontal flux as the reference over, for example,
the top step in the limb scan allows this simple form for
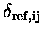 .
In order for equation (6.19) to be valid, the
altitude retrieval grid must possess a level at the altitude of the aircraft.
.
In order for equation (6.19) to be valid, the
altitude retrieval grid must possess a level at the altitude of the aircraft.
There are many techniques available to solve for 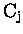 .
See Rodgers (1976) for a discussion of some of these.
If
.
See Rodgers (1976) for a discussion of some of these.
If
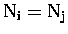 then a simple matrix inversion can be
performed,
then a simple matrix inversion can be
performed,
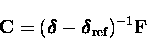 |
(11.21) |
where, for convenience, matrix notation is now used so that
F is the matrix form of F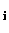 ,
C is the matrix form
of C
,
C is the matrix form
of C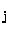 ,
and
,
and 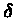 is the matrix form of
is the matrix form of
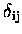 .
However, given noise on the measurements, this is likely to
produce a solution which is physically unrealistic and numerically
unstable.
For an over-constrained system,
.
However, given noise on the measurements, this is likely to
produce a solution which is physically unrealistic and numerically
unstable.
For an over-constrained system,
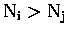 ,
least-squares or some other estimator can be used. In this case,
,
least-squares or some other estimator can be used. In this case,
![\begin{displaymath}{\b C}=[\DEL^T(\DEL-\DEL_{\rm ref})+\gamma
{\b H}]^{-1} \DEL^T {\b F}
\end{displaymath}](img636.gif) |
(11.22) |
where the superscript T denotes the matrix transpose.
In equation (6.22) an extra
term has been included,
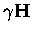 ,
which acts to constrain
the solution through the constraint matrix
,
which acts to constrain
the solution through the constraint matrix  and is coupled to
the solution by
and is coupled to
the solution by 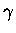 .
This added constraint is generally necessary as
unconstrained least squares is, as noted above, subject
to noise and oscillations in the solution.
Two common constraints are to minimize the first derivative of the
solution or to constrain to the climatological mean.
Drawbacks with this method are that it is not obvious what should be used
as the constraint or how tightly it should be coupled to the solution.
Constrained linear inversion is discussed in detail in Twomey (1977).
.
This added constraint is generally necessary as
unconstrained least squares is, as noted above, subject
to noise and oscillations in the solution.
Two common constraints are to minimize the first derivative of the
solution or to constrain to the climatological mean.
Drawbacks with this method are that it is not obvious what should be used
as the constraint or how tightly it should be coupled to the solution.
Constrained linear inversion is discussed in detail in Twomey (1977).
Another common technique is the method of maximum likelihood, or optimal
estimation. This method has the drawback of requiring an extensive
climatology for use as a priori profiles as well as the
covariance matrix.
As a third alternative, a non-linear iterative technique, such as Chahine's
method, can be employed (Chahine, 1977). In Chahine's method, an initial
guess for
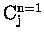 is made and equation (6.20) is evaluated.
An improved estimate is determined by,
is made and equation (6.20) is evaluated.
An improved estimate is determined by,
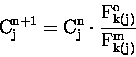 |
(11.23) |
such that,
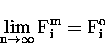 |
(11.24) |
where the superscript m refers to the modelled ACD, from
equation (6.20), and `o' refers to the observed ACD.
In practice the iterations are stopped once
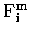 is within the uncertainties in
is within the uncertainties in
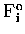 .
As with all methods of retrieval, it is essential that for a given
elevation angle there is a distinct peak in the weighting factors
as a function of height and that for different elevation angles
these peaks must occur at different heights.
This technique, using a weighted iteration formula,
was used by McKenzie et al. (1991) for the retrieval of
O3 and NO2 from zenith-sky DOAS.
.
As with all methods of retrieval, it is essential that for a given
elevation angle there is a distinct peak in the weighting factors
as a function of height and that for different elevation angles
these peaks must occur at different heights.
This technique, using a weighted iteration formula,
was used by McKenzie et al. (1991) for the retrieval of
O3 and NO2 from zenith-sky DOAS.
Testing of Chahine's method on synthetic spectra showed that it was
unable to retrieve the initial profiles, even with the weighted
iteration formula of McKenzie et al. (1991). Much better results were
obtained using a similar technique but
where the updated vertical column densities are
determined using an iterative least squares. This technique,
suggested by McDade and Llewellyn (1993) for airglow limb tomography and
adapted for CPFM limb scan retrievals,
has been found to be very robust and is well suited
to handling the similar weighting functions. In this method,
the vertical column densities are sought which minimize,
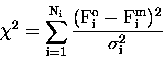 |
(11.25) |
where
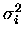 is the standard deviation of
is the standard deviation of
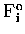 ,
a quantity obtained during the DOAS fitting process, and
,
a quantity obtained during the DOAS fitting process, and
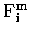 are calculated using equation (6.20). After each iteration,
the vertical column densities are calculated using,
are calculated using equation (6.20). After each iteration,
the vertical column densities are calculated using,
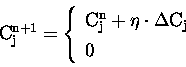 |
(11.26) |
such that always the larger is used,
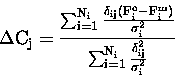 |
(11.27) |
and where,
![\begin{displaymath}\eta = \frac{ \rm\sum_{i=1}^{N_i} \left[ (F_i^o-F_i^m) \sum_{...
...=1}^{N_j} \frac{\delta_{ij} \Delta C_j}
{\sigma_i} \right]^2 }
\end{displaymath}](img648.gif) |
(11.28) |
is a damping factor.
Due to the similarity of the weighting functions for uplooking
angles, it is not possible to obtain significant vertical information
above the aircraft. However, they differ sufficiently for downlooking
angles, especially in the visible, that vertical information
below the altitude of the aircraft can be retrieved.
The retrieval method described above is applied as follows.
The vertical column below the aircraft
is obtained first using the nadir field with the horizontal flux
as the reference. Note that from Figure 6.12 and 6.13, the nadir
airmass factor above the aircraft is equal to
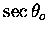 (where a value of
(where a value of
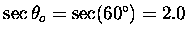 was used).
This implies that the absorption in the nadir field above the aircraft and the
absorption in the reference are essentially identical.
Also, as the nadir air mass
factor is nearly constant below the aircraft, the vertical profile of
the absorber below the aircraft is not required. This is less valid
in the near-UV where there is decreased sensitivity near the surface
(from Figure 6.13).
These points can be seen
using equation (6.20). For all layers above the aircraft,
was used).
This implies that the absorption in the nadir field above the aircraft and the
absorption in the reference are essentially identical.
Also, as the nadir air mass
factor is nearly constant below the aircraft, the vertical profile of
the absorber below the aircraft is not required. This is less valid
in the near-UV where there is decreased sensitivity near the surface
(from Figure 6.13).
These points can be seen
using equation (6.20). For all layers above the aircraft,
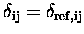 ,
and for the layers below the aircraft
,
and for the layers below the aircraft
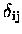 is constant (and
is constant (and
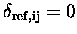 ).
Hence, equation (6.20) can be rearranged as,
).
Hence, equation (6.20) can be rearranged as,
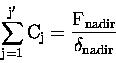 |
(11.29) |
where the left hand side is simply the vertical column below the
aircraft. A three-dimensional nadir air mass factor look-up table has been
created so that they need not be computed on-line.
The dimensions are solar zenith angle, surface albedo, and
altitude of the ER-2. Recall from Figures 6.12 and 6.13 that the
nadir air mass factor is largely independent of the height of the
absorbing layer.
The region in which the absorber is perturbed
is from the surface up to the altitude of the aircraft.
Tables were generated at the relevant wavelengths both with and without
ice and water droplets in the PBL and with background stratospheric
aerosols.
The second step is to obtain the column above the aircraft by performing
DOAS on the horizontal flux using an extra-terrestrial spectrum as the
reference. In this case, the column above the aircraft can be expressed
simply as,
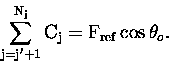 |
(11.30) |
The third step is to recover the vertical profile information.
Initially only four layers are used to represent the entire
atmosphere. Only four layers are used as with the large overlap and
small peaks of the weighting functions, it is expected that little
height information is contained in a limb scan.
The entire atmosphere above the aircraft is
taken as a single level and the atmosphere below the aircraft
is divided up into three layers. The best choice for these layers is
not clear, however, levels of 0-12, 12-16, and 16-
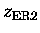 km
are initially chosen. These unequal divisions are used as the largest
gradients are expected between 12 and 20 km and so this will help
minimize the impact of the dependence of air mass factor on
the (unknown) profile through each layers.
Further, most of the information is expected to originate from
altitudes close to the aircraft.
km
are initially chosen. These unequal divisions are used as the largest
gradients are expected between 12 and 20 km and so this will help
minimize the impact of the dependence of air mass factor on
the (unknown) profile through each layers.
Further, most of the information is expected to originate from
altitudes close to the aircraft.
As an initial profile,
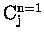 ,
for the layers below
the aircraft, a constant number density is used such that,
,
for the layers below
the aircraft, a constant number density is used such that,
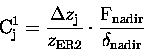 |
(11.31) |
and for the layer above the aircraft, the VCD obtained using the
horizontal flux is used.



Next: Simulations Using Synthetic Spectra
Up: Trace-Gas Retrievals
Previous: Calculation of Air Mass
Chris McLinden
1999-07-22
![]() represent the measured ACD at elevation angle i
and
represent the measured ACD at elevation angle i
and
![]() represent the ACD in the reference, initially
an unknown.
Hence the total ACD at elevation angle i is
represent the ACD in the reference, initially
an unknown.
Hence the total ACD at elevation angle i is
![]() .
This is related to the vertical column amounts through,
.
This is related to the vertical column amounts through,
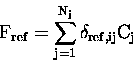
![]() .
See Rodgers (1976) for a discussion of some of these.
If
.
See Rodgers (1976) for a discussion of some of these.
If
![]() then a simple matrix inversion can be
performed,
then a simple matrix inversion can be
performed,
![]() is made and equation (6.20) is evaluated.
An improved estimate is determined by,
is made and equation (6.20) is evaluated.
An improved estimate is determined by,
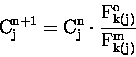
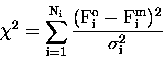
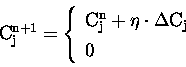
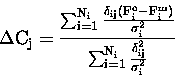
![\begin{displaymath}\eta = \frac{ \rm\sum_{i=1}^{N_i} \left[ (F_i^o-F_i^m) \sum_{...
...=1}^{N_j} \frac{\delta_{ij} \Delta C_j}
{\sigma_i} \right]^2 }
\end{displaymath}](img648.gif)
![]() (where a value of
(where a value of
![]() was used).
This implies that the absorption in the nadir field above the aircraft and the
absorption in the reference are essentially identical.
Also, as the nadir air mass
factor is nearly constant below the aircraft, the vertical profile of
the absorber below the aircraft is not required. This is less valid
in the near-UV where there is decreased sensitivity near the surface
(from Figure 6.13).
These points can be seen
using equation (6.20). For all layers above the aircraft,
was used).
This implies that the absorption in the nadir field above the aircraft and the
absorption in the reference are essentially identical.
Also, as the nadir air mass
factor is nearly constant below the aircraft, the vertical profile of
the absorber below the aircraft is not required. This is less valid
in the near-UV where there is decreased sensitivity near the surface
(from Figure 6.13).
These points can be seen
using equation (6.20). For all layers above the aircraft,
![]() ,
and for the layers below the aircraft
,
and for the layers below the aircraft
![]() is constant (and
is constant (and
![]() ).
Hence, equation (6.20) can be rearranged as,
).
Hence, equation (6.20) can be rearranged as,
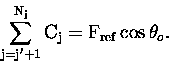
![]() km
are initially chosen. These unequal divisions are used as the largest
gradients are expected between 12 and 20 km and so this will help
minimize the impact of the dependence of air mass factor on
the (unknown) profile through each layers.
Further, most of the information is expected to originate from
altitudes close to the aircraft.
km
are initially chosen. These unequal divisions are used as the largest
gradients are expected between 12 and 20 km and so this will help
minimize the impact of the dependence of air mass factor on
the (unknown) profile through each layers.
Further, most of the information is expected to originate from
altitudes close to the aircraft.
![]() ,
for the layers below
the aircraft, a constant number density is used such that,
,
for the layers below
the aircraft, a constant number density is used such that,