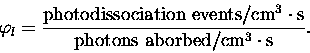Next: Scattering
Up: Basic Processes in Earth's
Previous: Photon Absorption
Photodissociation
A general photolysis reaction is written as,
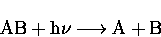 |
(3.18) |
which is the combination of two steps: the first is the
absorption of a photon, equation (2.17).
The second step, shown in Table 2.1, is an electronic
transition to an unbound excited state.
Kinetic energy may be imparted to the photolysis fragments and/or
they may be in an excited vibrational or electronic state.
Note that in some cases it is possible for photodissociation events to
occur upon photon fluorescence, an example of which is H2 in
Jupiter's atmosphere.
In general, the energy requirement is such that the absorption
must correspond to the excitation between electronic energy levels.
Minimum energies are 1 eV (election volt) or 2
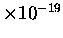 J,
which correspond to a wavelength of about 1
J,
which correspond to a wavelength of about 1 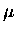 m.
m.
Photodissociation reactions are treated as elementary, or single-body,
reactions and their rate of chemical change can be quantified by
considering the rate of change in concentration of species l,
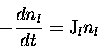 |
(3.19) |
where 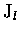 represents the photolysis rate constant (or J-value)
and has units of s-1.
Equation (2.19) admits the solution
represents the photolysis rate constant (or J-value)
and has units of s-1.
Equation (2.19) admits the solution
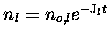 .
Thus, Jl-1 can be interpreted as the lifetime of species l
against photolysis. One major application of solar radiative transfer
is in the calculation of photolysis rate coefficients.
.
Thus, Jl-1 can be interpreted as the lifetime of species l
against photolysis. One major application of solar radiative transfer
is in the calculation of photolysis rate coefficients.
For a given wavelength interval, the J-value for species l is
proportional to the mean radiance, the absorption cross-section, and
the quantum efficiency. Considering the entire spectrum, the
total J-value is given by,
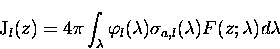 |
(3.20) |
where
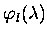 is the photolysis quantum yield for species l.
The factor of
is the photolysis quantum yield for species l.
The factor of 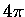 arises from the definition of the mean radiance.
Equation (2.20) represents
the probability that the absorption of a single photon will
lead to a photodissociation event. It is defined mathematically as,
arises from the definition of the mean radiance.
Equation (2.20) represents
the probability that the absorption of a single photon will
lead to a photodissociation event. It is defined mathematically as,
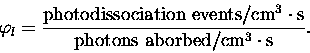 |
(3.21) |
Quantum yield is a molecular property which can be measured through
laboratory experiments and, in general, depends on pressure,
temperature, and wavelength.
Note that Jl is independent of the concentration of species l
except when absorption is significant enough to affect the
mean radiance or if the cross-section or quantum yield are
pressure dependent (e.g.: O2 at high pressure).



Next: Scattering
Up: Basic Processes in Earth's
Previous: Photon Absorption
Chris McLinden
1999-07-22
![]() J,
which correspond to a wavelength of about 1
J,
which correspond to a wavelength of about 1 ![]() m.
m.